テレビで『マンゴー』を簡単に皮むきする方法が紹介されていた。youtubeでも同じ内容のものが結構あったので紹介しておこう。

　この方法がすごく便利なのかはわからない。少なくともぼくにとってはどうでもいいようだ。だいたいマンゴーをそれほど食べる機会がない。沖縄に行った時、現地のお土産の形のいいマンゴーが、とても高価そうに熟して、案の定確かに高価だったのを覚えている。産地だからいいものが破格に安く買えるという甘い期待を、 甘いマンゴーは裏切ってくれた。その昔のマスクメロンと同じ感覚だ。 僕の子ども時代、父や母がたいへん世話になったらしい”えらい”人の病気のお見舞いとかでしか見ることもなかった。桐の箱に入っていた感じがするが、記憶違いかも知れない。本当に果物はピンキリだ。上質のものは美味しさも値段も桁違いだ。その沖縄で,数個お土産で”えらい”人に送り、私は、現地のスーパーで、もとは高級なマンゴー の見切り品をとても安く買って、ホテルの部屋で食べた。最高に美味かったのを覚えている。あと1日たつと売り物にならないものだったのだろう。残念ながら”えらくない”私には、誰も送ってくれる人がいない。(笑)

　さて、このマンゴー、3枚にカットした切り口は楕円になっている。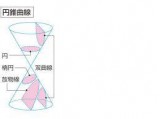
楕円は座標平面上でx、yの二次式で表されるから二次曲線と言うが、他の二次曲線 双曲線、放物線も合わせて円錐曲線とも呼ばれる。これはそれぞれの曲線がいずれも円錐を一つの平面で切った切り口の形になっているからである。番組を見ながらこんな図が頭に浮かぶ。

　　　　　　　「そうか！」

　コップを斜めに切った切り口の曲線が楕円なのだ。だから斜めにコップにあてながら押していくと、見事に剥けるのだな。

　この「便利な」マンゴーの皮むき‥‥、誰かが偶然発見したのか、手当たり次第やってみて見つけたのか、いや理論(?)が先か、果てまた、その科学的(？)根拠は未だ解明されていないのか？ アボガドへの転用は？

  まあ何事も実証的に‥‥。近くのスーパーでお買い得のマンゴーを買ってやってみた。     そんなに華麗にはいかない。数学的考察も関係ないようだ。いずれにしろぼくにはこれ以上はどうでもいいことかも知れない。(笑)

美味しかった

削ぎ落として

切り口は楕円に近い

楕円球にしては少し不恰好