スーパーで売っていたので買ってみた。イタリア料理にはよく使われるようで本名はBroccolo Romanesco（ブロッコロ・ロマネスコ） ローマのブロッコリーの意味だが、カリフラワーの仲間でアブラナ科の黄緑色の野菜だ。その形から「サンゴ礁」とも呼ばれる。

  子どもたちは、「うァ〜 キモい。 何なの？」と言って少し距離を置いて見てから近づいてくる。私はフキノトウのようにその鮮やかな黄緑色に初春を感じる。

  円錐型の小さな突起が螺旋状に集まって大きな形をつくり、さらにそれが集まって同じ円錐上に螺旋を描く。
何かの中に同じ何かがある、または何かが集まって同じような何かができることが「自己相似」で、このロマネスコのように特に図形的な自己相似形を「フラクタル」という。1982年フランスの数学者マンデンブロが「フラクタル幾何学」の理論を発表した。このフラクタル図形は、このロマネスコを初めとし、例えば海岸線やシダの葉など、自然界にも存在する。(ロマネスコは人工的につくったものらしいが)

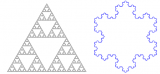有名な数学のフラクタル図形である。左がシェルピンスキーのガスケット(穴が空いた同名の機械部品に見えることから)、右はコッホ曲線(雪の結晶に見えることからコッホ雪片とも言われる)という。例えばコッホ曲線は次のように作図する。

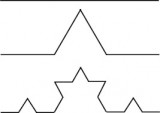  線分を三等分して、真ん中の線分を一辺とする正三角形を上側(外側)につくり、下の線を消す。新しくできた2本の線分を三等分して、真ん中の線分を一辺とする正三角形を外側につくり、一本の辺を消す。これを無限に繰り返す。

 これらの図形は、自由度が高い中学入試や大学入試でたびたび題材に使われる。いや使われた。入試問題も流行がある。フラクタルが何かと話題になった十数年前に多かった。例えば中学入試では、コッホ曲線の作図のプロセスを数回行った結果できる正三角形の面積を求めるなど、規則性と求積の問題の題材になる。また、大学入試問題では、操作を無限に繰り返すので、等比数列や極限の問題になる。いずれも作問の意図はそう変わらない。

  はて、このロマネスコを観察し、思索を巡らせた後、茹でてパスタに入れて食べた。甘みがあって美味しかった。

パーニャカウダーのディップをつけて

ペパロンチーノ風withアンチョビー